|
|
在刷10-4e的时候发现手枪人形会打出2点伤害的暴击,发现暴击判定是在扣减护甲之后进行。
因此想到自己在之前那个[8-1N平A AR带队分析]里的计算模型存在严重问题。 真鸡儿丢人 瞎
而之前看了[关于伤害浮动参数[0.85-1.15]的研究]这一个帖子之后也有所启发
在此决定重新考虑少前中伤害机制的分布问题并尝试建立一个数学模型,来计算伤害的分布。
通篇理论自嗨,各位可以直接移步应用部分查看计算结论哭笑
先说公式:
此处关于护甲的部分参考了彩虹佬的帖子[新版本护甲系统变动与护甲属性的个人见解]
少前的伤害计算公式大致总结如下:

注意此处变量都是考虑光环技能等加成的实际数值
ceil为向上取整函数
− 数学建模(未考虑上取整函数影响) ...
我们做如下三条合理假设:
1. 满扩人形一次射出的五发子弹每一发可视为独立事件
2. 子弹的伤害波动与是否暴击两事件之间无相关性。
3. 子弹的伤害波动遵循均匀分布。
而子弹是否暴击这一事件理论上遵循成功率为CR=CritRate(暴击率)的伯努利分布。
则单个人形单发子弹的伤害X可表示为子弹伤害变量H和子弹暴击倍率变量C组成的以下模型:(暂不考虑上取整操作)

由于变量H遵循均匀分布,变量C遵循伯努利分布(可视为n=1的二项分布),因此可计算H、C的期望及方差如下,同时根据H、C的期望及方差计算单个人形单发伤害X的期望。

而X的方差计算较为复杂:

表示满扩人形5发子弹总伤害的随机变量X':

上取整操作对于伤害期望的影响及修正 ...
对于非暴击伤害期望,由于伤害为均匀分布,向上取整操作可视为增加0.5的伤害期望。
观察下图中蓝色条形图与红色实线下方面积差异可知,在x轴每一个单位长度上均多出一个面积为0.5的小三角形,因此: Eceil(H) = E(H) +0.5

对于暴击伤害期望,取整运算的影响比较复杂。
由于爆伤倍率是0.01的整数倍,因此x点伤害和(x+100)点伤害在计算爆伤之后的小数部分必定是一致的,因此上取整操作增加的量也是一致的,从而上取整操作增加的量形成一个最长周期为100点伤害的循环,而若是爆伤倍率*100与100的公约数更大,循环的周期就更短。
单个循环内,上取整的增加总量是固定的。
上图是1.5倍爆伤的周期,可看到在奇数点伤害时,暴击后上取整(绿色方块)比取整伤害乘暴击(绿色虚线)高出0.5个单位,而在偶数点伤害时,由于1.5*2k=3k,因此上取整操作不增加值,绿色方块和绿色虚线高度一致。
易推出若暴击周期为n(可知n为100/GCD(爆伤倍率*100, 100)),则增加的暴击伤害期望如下:

下图是1.6倍爆伤时的取整示意图,可看到未暴击打出5点伤害时暴击伤害正好为8点,达成长度为100/GCD(160,100)= 5的循环,在这个循环内,上取整操作分别增加了0.6, 0.4, 0.2, 0.8, 0点伤害
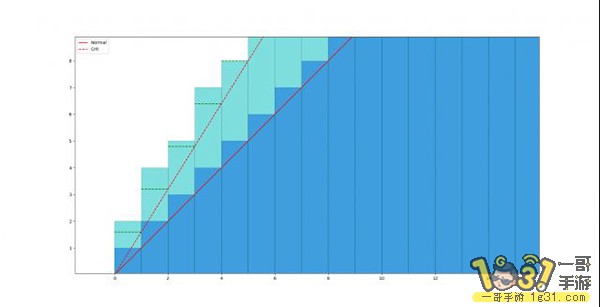
上取整操作对于方差的影响不大,可以忽略不计
− 利用模拟数据对这一理论模型进行验证 ...
按照上述的伤害模型,数值设定为100火力,0护甲,0穿甲,0.68暴击率,1.5爆伤倍率,模拟10,000,000次伤害,绘制理论分布曲线X~N(5E(X), 5D(X))以及由模拟结果拟合的正态分布曲线
概率密度分布如下图:

图中红色曲线为按上述期望及方差绘制的正态分布概率密度曲线,蓝色曲线为由模拟结果拟合的正态分布曲线,可看出两条曲线基本重合。模拟结果的频率数据点则稍有偏差。
而三者的累积分布函数曲线CDF则基本重合,如下图所示:
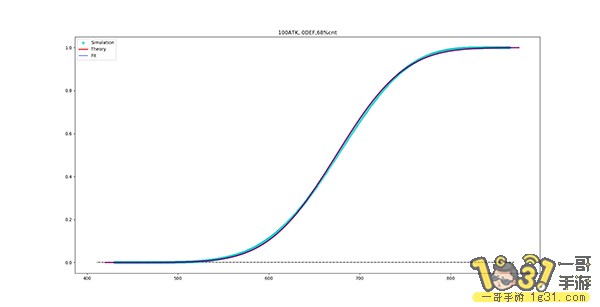
理论分布及数据拟合的正态分布函数特征值及分位函数值如下:
理论分布: mu=674.2000, sigma=58.6602, Variance=3441.0180,分位函数ppf(0.001)=492.9264
数据拟合1: mu=674.1918, sigma=58.8873,Variance=3467.7194,分位函数ppf(0.001)=492.2162
数据拟合2: mu=674.1827, sigma=58.8926,Variance=3468.3398,分位函数ppf(0.001)=492.1908
可看出我们所设计的理论模型可以很好的反映实际的分布情况,模拟结果的数据点有偏差可能是由于模拟结果的取值存在上下界而正态分布理论上范围为整个数轴,而使得模拟结果分布较为集中。
而在下面即将提及的应用部分中,我们对理论分布取分位函数的操作也可以保证实际中的准确度。
− 实际应用:8-1N与10-4e ...
根据如上模型,我们在面对特定敌人时即可计算所需的火力暴击率或爆伤等等光环(主要的使用还是计算火力)
计算方式为预设理论火力上下限,采用二分法逼近。
取上下限的中值计算理论伤害分布,比较理论伤害分布的分位函数ppf(0.001)=mu-3.0902sigma 与目标HP的大小,若大于HP则将中值设为新的上限,小于HP则将中值设为下限,循环逼近直至上下限差距小于等于1,此时取上限作为目标结果。
这样计算出的火力值能保证99.9%几率击杀敌人 千分之一的翻车几率
应用1:之前8-1N的平A AR带队伤害计算
敌人78HP,5编制,104护甲 我方10穿甲。
火力AR两枪一狗,射速AR一枪一狗,暴击率光环和对应火力需求如下表:
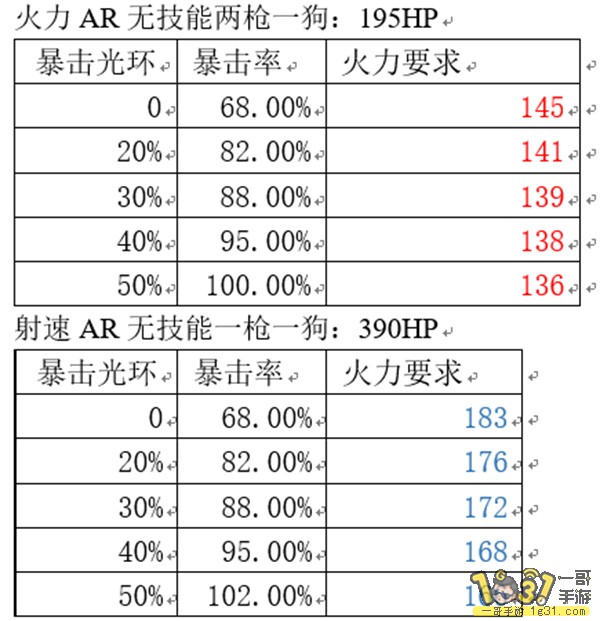
应用2:10-4e小公主刷核心
敌人9000HP,199护甲 我方10穿甲。其余参数设定为68%的暴击率和1.5的爆伤, 由于伤害占大头的炮击直伤不受暴击影响因此给小公主配暴击光环和爆伤光环的意义不大
目标是小公主一炮打掉一个绿无敌,即目标9000HP
由咖啡dalao的测试贴[[撇个砖头] m4a1改造2技能机制]可知:
M4二技能600%的炮击直伤不受暴击影响,100%的溅射存在暴击加成,两者均受护甲影响
此时M4单个人形单发伤害相当于一发600%火力,0暴击率的炮击伤害与一发100%火力正常暴击率的子弹伤害叠加,随机变量算式增加炮击伤害H’,相关计算如下:

经测试,炮击伤害与溅射伤害的浮动系数并不相等,我们可以简单的假设二者独立,见下图:

根据修改后的Xm4期望和方差,重新设定理论分布,求得所需火力341
在10-4e,小公主有地图优势20%加成,默认带灰熊光环30%加成,技能25%,自身一技能75%加成,除去这部分加成,面板火力应为341/(1.2*1.3*1.25*1.75)=100。
100点伤害是编成面板的数值要求,即考虑了好感度、装备及妖精光环的数值
换句话说你要是编成面板看小公主有100点火力以上就可以愉快的去10-4e了 记得带满技能灰熊和满技能射速手枪
有人反映编成面板96点火力也比较稳定
|
|