[换个角度][施工ing...]俄罗斯方块培养攻略(5*6+6更新42组非镜面解)

只谈正事

本文仅仅对于“如何使用五星五格一类/五星六格的小方块铺满6*6格子”进行讨论 不就属性基值问题进行讨论

55楼更新纯五星六格拼法

等回去摸下电脑 拿excel再弄好看一下

一. 推荐使用6个五星五格一类+1个

论证过程

只有五星六格/五星五格一类的密度补正为1.0 达到最大值 故仅讨论使用上述两种方格密铺6*6格子的问题

设x为五星五格一类数量 y为五星六格数量 则有5x+6y=36
x应当是6的倍数 解得
x1=0 y1=6
x2=6 y2=1
考虑到向上取整 第二组解大于第一组的次数 总属性等级大于等于第一组
故本文先对第二组解进行构造

二. 推荐芯片培养顺序

之前的版本(已经不需要了)

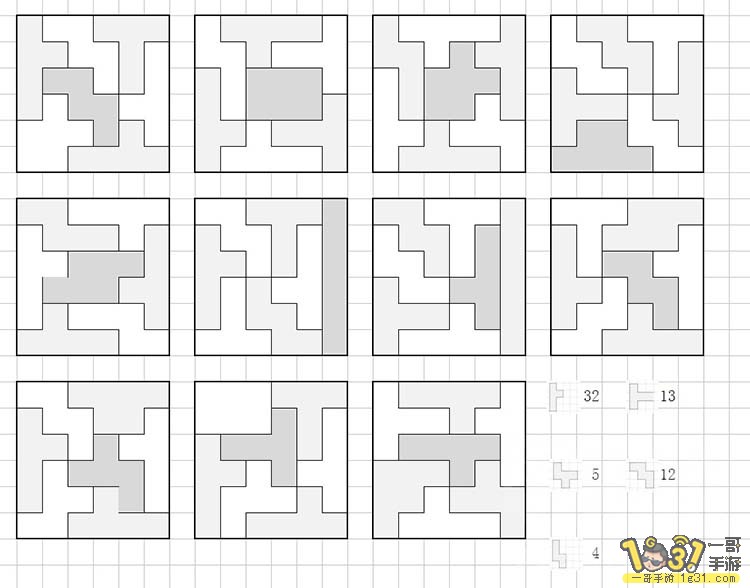
如图，目前构造了11组不同的密铺方式，对各个芯片出现次数进行讨论：
14的芯片出现次数最多 共32次。即使有两种不同形状 仍然推荐优先培养
113的芯片出现其次多 共13次。推荐优先培养
221的芯片和前者势均力敌 共12次。 推荐优先培养
剩下两种均有出现 可以预留着 对属性较好的进行培养
131(十字)没有出现 不必要培养
六格的芯片 按照已有的五个芯片属性&数量 选择较为匹配的进行培养

− 比较全的42组非镜面解&新的结论 ...

为了节省地方 有些图上不止一组解；
w为“221” t为“113” +为十字“131”
某某+代表形状中的(1-3L)型顺时针的 某某-代表逆时针

14+ *:** ; 14- **:*
23+ ,:** ; 23- **:,

将所有的对应的“+”和“-”互换 为镜面结果

使用24(t)的11种解(镜面22组)
[url=][/url]
[url=][/url]

使用6(l)的10组解(镜面20组)
[url=][/url]
[url=][/url]

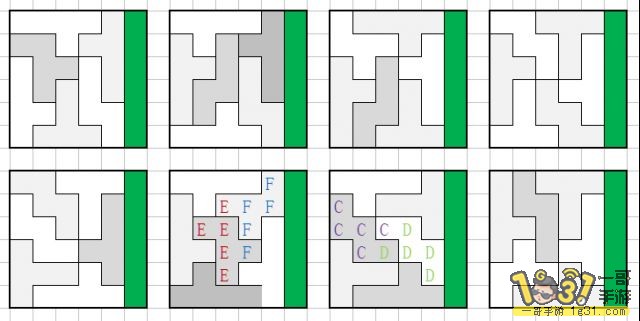
使用123(w)的10组解(镜面20组)
[url=][/url]
[url=][/url]

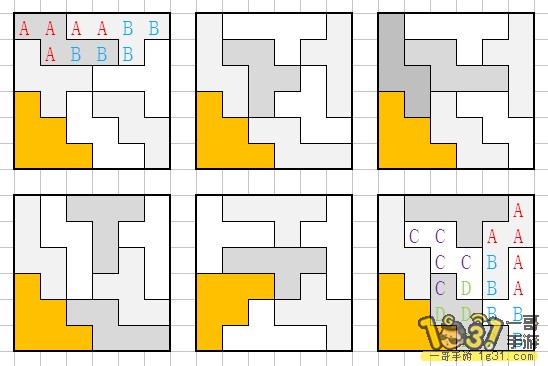
使用33(矩形)的2组解(镜面4组)
[url=][/url]
[url=][/url]

使用33(z)的4组解(镜面8组)
[url=][/url]
[url=][/url]

使用132(鱼)的5组解(镜面10组)
[url=][/url]

[url=][/url]