|
本文仅仅对于“如何使用五星五格一类/五星六格的小方块铺满6*6格子”进行讨论 不就属性基值问题进行讨论
55楼更新纯五星六格拼法 等回去摸下电脑 拿excel再弄好看一下
一. 推荐使用6个五星五格一类+1个
− 论证过程 ...
只有五星六格/五星五格一类的密度补正为1.0 达到最大值 故仅讨论使用上述两种方格密铺6*6格子的问题
设x为五星五格一类数量 y为五星六格数量 则有5x+6y=36
x应当是6的倍数 解得
x1=0 y1=6
x2=6 y2=1
考虑到向上取整 第二组解大于第一组的次数 总属性等级大于等于第一组
故本文先对第二组解进行构造
二. 推荐芯片培养顺序
− 之前的版本(已经不需要了) ...

如图,目前构造了11组不同的密铺方式,对各个芯片出现次数进行讨论:
14的芯片出现次数最多 共32次。即使有两种不同形状 仍然推荐优先培养
113的芯片出现其次多 共13次。推荐优先培养
221的芯片和前者势均力敌 共12次。 推荐优先培养
剩下两种均有出现 可以预留着 对属性较好的进行培养
131(十字)没有出现 不必要培养
六格的芯片 按照已有的五个芯片属性&数量 选择较为匹配的进行培养
− 比较全的42组非镜面解&新的结论 ...
为了节省地方 有些图上不止一组解;
w为“221” t为“113” +为十字“131”
某某+代表形状中的(1-3L)型顺时针的 某某-代表逆时针
14+ *:** ; 14- **:*
23+ ,:** ; 23- **:,
将所有的对应的“+”和“-”互换 为镜面结果
使用24(t)的11种解(镜面22组)

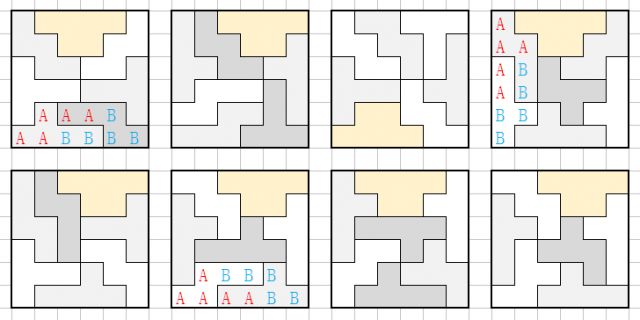
使用6(l)的10组解(镜面20组)


使用123(w)的10组解(镜面20组)

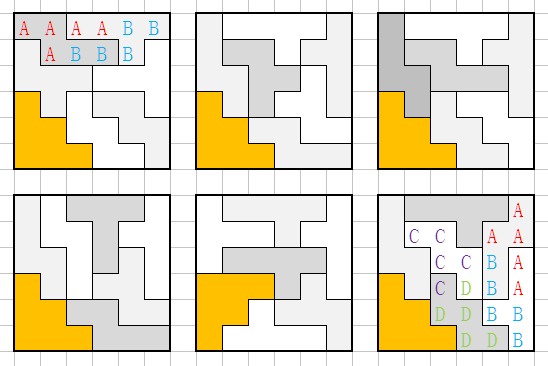
使用33(矩形)的2组解(镜面4组)


使用33(z)的4组解(镜面8组)
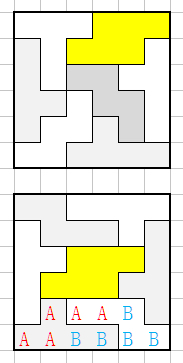

使用132(鱼)的5组解(镜面10组)

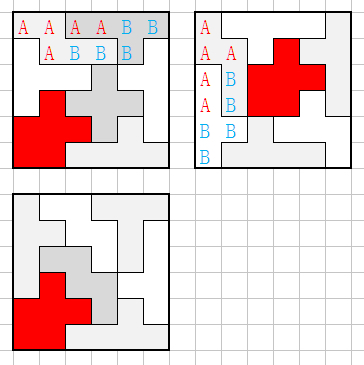
新的结论
w型:15+8+10+0+2+2=37
t型:9+11+4+4+1+3=32
14+-:(12+16+7+3+5+12)+(15+12+12+3+10+5)= 60+57 = 117
23+-:(7+4+11+1+3+2)+(2+3+6+0+3+2)= 28+16 = 44
“+”:2
131+-:(1+4+7+1+0+0)+(4+3+3+0+0+2)= 13+12 = 25
可以发现:14出现次数仍然最多 仍然推荐培养;取镜面可以发现单个14除了某两个都出现过 所以至少强化一个;推荐强化:2个某方向 + 1个相反的方向
其次:23出现的次数也很多;在14出现时,+/-中出现较多的,出现的同号的23概率大于异号23;推荐强化:和之前两个14同方向的23 强化一个
再者:w和t型均出现较多;推荐各强化一个
最后 根据拥有的剩下的方块,决定最终方案
− 举个例子 ...
选择两个顺时针的14 一个逆时针的14 一个顺时针的23 一个w 一个t
那么要凑齐6个5格+1个6格 且能拼成6*6还需要的五格数量:2/2/1/3/1/2/2/1/1/2/2;1/2/2/2/2/3/2/2/1;2/2/3/2/3/2/2/2/3/3;2/1;1/3/2/2;2/1/2/2/1
如上 均选择了两种镜面中更适合的 平均还需要强化次数略小于2,即平均需要比“刚好抽到需要的六个五格”多强化1个不到 这种强化方式灵活性极大 在期望以内(可能还有更优的强化解 但是浪费1个之内算是可以接受吧....)
三. 一些碎碎念
− ... ...
1. 其实如果考虑使用一个五星五格二类的话 会舒服很多。很多。。很多。。。
即便会亏一些属性 也比用三四格的来凑要高一些
2. 有没有大佬帮忙写个程序呢..?
3. 这种东西 放到官方那个攻略征集有用嘛...就这几个字 不过或许可以roll到..?
4. 纯五星六格的 已经在做了 咕咕咕咕咕
四. 特别鸣谢 各位提供数据的大佬们;各位提供程序的大佬们;以及其他研究这个问题给予我灵感的大佬们 谢谢谢谢大家orz
|